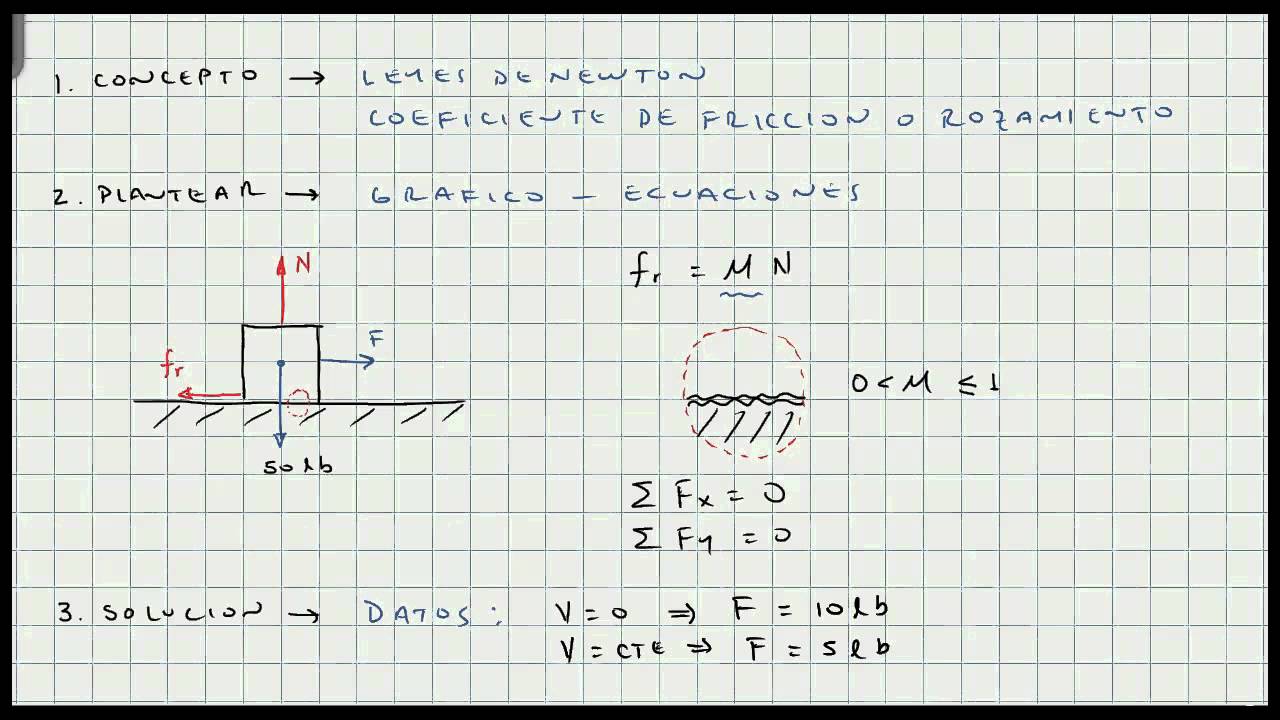
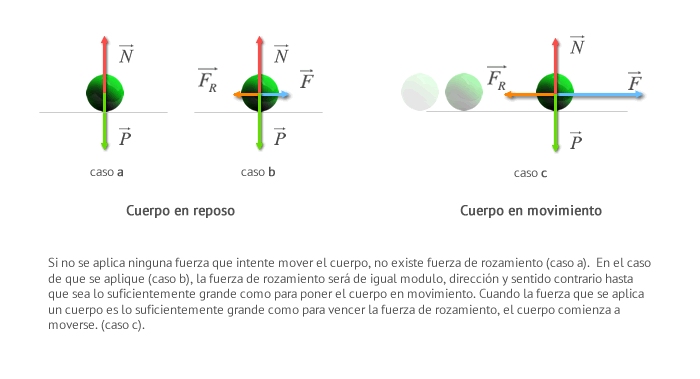
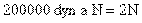Problemas De Rozamiento o Friccion

1.-

2.-



3.-

Problemas De Trabajo, Energia Y Potencia

Trabajo, Energia Y Potencia

Rozamiento O Fricción

¿Qué es la fuerza de rozamiento o de fricción?

Si empujas una bola sobre una superficie, esta terminará parándose en algún momento. ¿No contradice este fenómeno al Principio de Inercia?. Como no se le aplica ninguna fuerza, ¿No debería seguir moviéndose indefinidamente?

La cuestión a esa pregunta es bien sencilla. El hecho de que la bola se termine parando no contradice este Principio, ya que durante su movimiento existe una fuerza "invisible" que provoca que la velocidad de la pelota vaya disminuyendo: la fuerza de rozamiento. La bola al desplazarse sobre el suelo roza contra él y contra el aire. Este rozamiento produce una pareja de fuerzas que "tiran" en contra del movimiento. 

La fuerza de rozamiento o de fricción (FR−→) es una fuerza que surge por el contacto de dos cuerpos y se opone al movimiento.

El rozamiento se debe a las imperfecciones y rugosidades, principalmente microscópicas, que existen en las superficies de los cuerpos. Al ponerse en contacto, estas rugosidades se enganchan unas con otras dificultando el movimiento. Para minimizar el efecto del rozamiento o bien se pulen las superficies o bien, se lubrican, ya que el aceite rellena las imperfecciones, evitando que estas se enganchen.

¿No has patinado nunca sobre un suelo recién pulido o encerado? ¿A que no tienes que hacer a penas fuerza para desplazarte bien lejos?

Características de la fuerza de rozamiento o de fricción

A grandes rasgos, las características de la fuerza de rozamiento se pueden resumir en los siguientes puntos:

• Se opone al movimiento de un cuerpo que se desliza en contacto con otro. 
• Depende de 2 factores:
  • la naturaleza de los materiales que se encuentran en rozamiento y el tratamiento que han seguido. Este factor queda expresado por un valor numérico llamado coeficiente de rozamiento o de fricción.
  • la fuerza que ejerce un cuerpo sobre el otro, es decir, la fuerza normal.

¿Cómo se calcula la fuerza de rozamiento o de fricción?

Cuando el cuerpo está en reposo

La fuerza de rozamiento tiene el mismo módulo, dirección y sentido contrario de la fuerza horizontal (si existe) que intenta ponerlo en movimiento sin conseguirlo.

Cuando el cuerpo está en movimiento

Como la fuerza de rozamiento depende de los materiales y de la fuerza que ejerce uno sobre el otro, su módulo se obtiene mediante la siguiente expresión:

Fr=μ⋅N

donde:

• FR es la fuerza de rozamiento
• μ es el coeficiente de rozamiento o de fricción
• N es la fuerza normal

Problemas de La Segunda Condición De Equilibrio

Ejemplo 1

Encontrar la magnitud de una tercera fuerza F3, que aplicada a dos metros del eje de giro del aspa que se muestra en la siguiente figura se encuentre en equilibrio rotacional.

SOLUCIÓN 

Aplicamos la segunda condición del equilibrio y sumamos todos los momentos en el eje de rotación:

Ejemplo 2

Una barra sin peso se mantiene en equilibrio, tal como se muestra en la figura. Hallar el valor del peso w

SOLUCIÓN

En el diagrama de cuerpo libre se puede apreciar la fuerza R que es la fuerza de reacción que ejerce el soporte sobre la barra. Aplicando la segunda condición del equilibrio sobre el punto R tenemos que:

Segunda condición de equilibrio

Un cuerpo se encuentra en equilibrio de rotación si el momento resultante de todas las fuerzas que actúan sobre él, respecto de cualquier punto, es nula.

Matemáticamente, para el caso de fuerzas coplanares, se debe cumplir que la suma aritmética de los momentos relacionados con rotaciones antihorarias debe ser igual a la suma aritmética de los momentos relacionados con rotaciones horarias.

Para que un cuerpo esté en equilibrio de rotación, debe cumplirse la segunda condición que dice: para que un cuerpo esté en equilibrio de rotación, la suma de los momentos o torques de fuerzas que actúan sobre él respecto a cualquier punto debe ser igual a cero. Es decir:

Matemáticamente, para el caso de fuerzas coplanares, se debe cumplir que la suma aritmética de los momentos relacionados con rotaciones anti-horarias debe ser igual a la suma aritmética de los momentos relacionados con rotaciones horarias.

En general, un cuerpo se encontrará en equilibrio traslacional y equilibrio rotacional cuando se cumplen las dos condiciones de equilibrio.

Problemas Sobre La Primera Condición Del Equilibrio

Una pelota de 300N cuelga atada a otras dos cuerdas, como se observa en la figura. Encuentre las tensiones en las cuerdas A, B Y C.

 

SOLUCIÓN:

El primer paso es construir un diagrama de cuerpo libre:

Al sumar las fuerzas a lo largo del eje X obtenemos :

S Fx = -A cos 60° + B cos 40° = 0

Al simplificarse por sustitución de funciones trigonométricas conocidas tenemos:

-0.5A + 0.7660B = 0 (1)

Obtenemos una segunda ecuación sumando las fuerzas a lo largo del eje Y, por lo tanto tenemos:

(Cos 30° + cos 50° )

0.8660A + 0 .6427B = 300N (2)

En las ecuaciones 1 y 2 se resuelven como simultanea A y B mediante el proceso de sustitución. Si despejamos A tenemos:

A = 0.7660 / 0.5

 

A = 1.532B

Ahora vamos a sustituir esta igualdad en la ecuación 2

0.8660(1.532B) + 0.6427B = 300N

Para B tenemos:

1.3267B + 0.6427B = 300N

 

1.9694B = 300N

B= 300N / 1.9694

 

B= 152.33N

Para calcular la tensión en A sustituimos B = 152.33 N

A = 1.532(152.33N) = 233.3N

La tensión en la cuerda C es 300N , puesto que debe ser igual al peso.

2. Una pelota de 100N suspendida por una cuerda A es tirada hacia un lado en forma horizontal mediante otra cuerda B y sostenida de tal manera que la cuerda A forma un ángulo de 30° con el poste vertical ¿ encuentre las tensiones en las cuerdas A y B.

 

SOLUCIÓN

Primero dibujamos le diagrama cuerpo libre:

Ahora se aplica la primera condición de equilibrio. La suma de las fuerzas a lo largo del eje X:

SFx = B – A cos 60° = 0

B = A cos 60° = 0.5 A (1)

Ahora al sumar las componentes en Y:

S Fy = A sen 60° - 100N = 0

Por lo que:

A sen 60° = 100N

Ahora se despejan las fuerzas desconocidas:

(sen 60° = .8660)

.8660 A = 100N

A = 100N / .8660 = 115N

Conocemos el valor de A, ahora despejamos B de la ecuación 1:

B = 0.5 A = (0.5)(115N) = 57.5N

La Primera Condicion de Equilibrio 

Un cuerpo se encuentra en estado de equilibrio traslacional si y sólo si la suma vectorial de las fuerzas que actúan sobre él es igual a cero.

Cuando un cuerpo está en equilibrio, la resultante de todas las fuerzas que actúan sobre él es cero. En este caso, Rx como Ry debe ser cero; es la condición para que un cuerpo esté en equilibrio:

 

Problemas Aplicados A Las Leyes de Newton

• 1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.

Datos

m = 2,5 Kg.

a =1,2 m/s2.

F =? (N y dyn)

Solución

Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)

Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:

 Sustituyendo valores tenemos:

 

Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:

• 2. ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?

Datos

a =?

m = 2,5 Kg.

F = 200000 dyn

Solución

La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.

Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

 

 La ecuación de la segunda ley de Newton viene dada por:

 Despejando a tenemos:

 Sustituyendo sus valores se tiene:

 

• 3. Un cuerpo pesa en la tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la gravedad es 1,6 m/s2?

Datos

PT= 60 Kp = 588 N

PL =?

gL = 1,6 m/s2

Solución

Para calcular el peso en la luna usamos la ecuación

 

Como no conocemos la masa, la calculamos por la ecuación:  que al despejar m tenemos:

 

Esta masa es constante en cualquier parte, por lo que podemos usarla en la ecuación (I):

• 4. Un ascensor pesa 400 Kp. ¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.

Solución

Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.

 

La fuerza resultante que actúa sobre el ascensor es F – P

Aplicando la ecuación de la segunda ley de Newton tenemos:

Al transformar 400 Kp a N nos queda que:

400 Kp = 400 ( 9,8 N = 3920 N

Sustituyendo los valores de P, m y a se tiene:

F – 3920 N = 400 Kg. ( 0,5 m/s2

F – 3920 N = 200 N

Si despejamos F tenemos:

F = 200 N + 3920 N

F = 4120 N

• 5. Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?

Solución

En la figura 8 se muestran las condiciones del problema

 

La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.

Si aplicamos la segunda ley de Newton se tiene:

Sustituyendo F, m y a por sus valores nos queda

80 N – Fr = 25 Kg. ( 0,5 m/s2

80 N – Fr = 12,5 N

Si despejamos Fr nos queda:

Fr = 80 N – 12,5 N

Fr = 67,5 N