Velocidad y Aceleración angular MCU y MCUV

MCUA, desplazamiento, Velocidad y Aceleración Angular

Velocidad y Aceleración angular MCU y MCUV

Velocidad Angular

La velocidad angular es una medida de la velocidad de rotación. Se define como el ángulo girado por unidad de tiempo y se designa mediante la letra griega . Su unidad en el Sistema Internacional es el radiansegundo (rad/s). La velocidad angular es la variación del desplazamiento angular por unidad de tiempo:

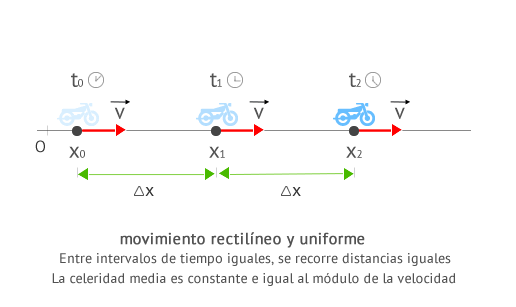
Partiendo de estos conceptos se estudian las condiciones del movimiento circular uniforme, en cuanto a su trayectoria y espacio recorrido, velocidad y aceleración, según el modelo físico cinemático.

Aceleración Angular

Aceleración angular es el índice del cambio de velocidad angular encima tiempo. En SI las unidades, se mide adentro radianes por en segundo lugar ajustado (rad/s2), y es denotado generalmente por la letra griega alfa (α). El movimiento circular se clasifica de acuerdo a la ausencia o presencia de ”la aceleración tangencial uniformemente circular “(MCU) y  con un movimiento circular uniformemente variado (MCUV).

En el movimiento plano del sólido rígido, la aceleración angular, al igual que la velocidad angular, tiene la dirección del eje de rotación y viene dada por:

donde   representa el ángulo girado en función de t y ω la velocidad angular.

En el movimiento plano tanto la velocidad angular como la aceleración angular son vectores perpendiculares al plano en el que se produce el movimiento.

Problemas de Movimiento Angular

PROBLEMA 1

Un carro de juguete que se mueve con rapidez constante completa una vuelta alrededor de una pista circular (una distancia de 200 metros) en 25 seg.

a) Cual es la rapidez promedio?

b) Si la masa del auto es de 1,5 kg. Cual es la magnitud de la fuerza central que lo mantiene en un circulo?

a) Cual es la rapidez promedio?

b) Si la masa del auto es de 1,5 kg. Cual es la magnitud de la fuerza central que lo mantiene en un circulo? L = 200 metros = 2 π r

Despejamos el radio

F = 3,01 Newton

PROBLEMA 2

En un ciclotrón (un tipo acelerador de partículas), un deuterón (de masa atómica 2u ) alcanza una velocidad final de 10 % de la velocidad de la luz, mientras se mueve en una trayectoria circular de 0,48 metros de radio. El deuterón se mantiene en la trayectoria circular por medio de una fuerza magnética. Que magnitud de la fuerza se requiere?

Velocidad de la luz = 3 X 108 m/seg

Velocidad del deuterón = 3 X 107 m/seg

Masa deuterón 2u = 2 * 1,661 X 10-27 kg.

Masa deuterón 2u = 3,322 X 10-27 kg.

F = 6,2287 * 10-12 Newton

Leer más: http://www.monografias.com/trabajos38/movimiento-circular/movimiento-circular2.shtml#ixzz4dzPygafI

Problemas de Movimiento Circular, Aceleración y Fuerzas Centrípetas

Problema II

Cualquier movimiento sobre un camino curvo, representa un movimiento acelerado, y por tanto requiere una fuerza dirigida hacia el centro de la curvatura del camino. Esta fuerza se llama fuerza centrípeta, que significa fuerza "buscando el centro". La fuerza tiene la magnitud

El balanceo de una masa en una cuerda requiere tensión en la cuerda, y si la cuerda se rompe, la masa recorrerá un camino tangencial en línea recta.

La aceleración centrípeta se puede derivar para el caso de movimiento circular puesto que el camino curvado en cualquier punto, puede extenderse hasta formar un círculo.

Note que la fuerza centrípeta es proporcional al cuadrado de la velocidad, con lo que doblando la velocidad necesitará cuatro veces la fuerza centrípeta para mantener el movimiento en un círculo. La fuerza centrípeta la tiene que proporcionar la fricción a lo largo de la curva. Si esta fricción es insuficiente un incremento de la velocidad nos puede llevar a un derrape inesperado.

Movimiento Circular, Aceleración y Fuerzas Centrípedas

Movimiento circular

En cinemática, el movimiento circular (también llamado movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de giro es constante (giro ondulatorio), se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio, centro fijo y velocidad angular constante.

La Aceleración

En física, la aceleración es una magnitud vectorial que nos indica la variación de velocidad por unidad de tiempo. En el contexto de la mecánica vectorial newtoniana se representa normalmente por ${\displaystyle {\vec {a}}\,}$ o ${\displaystyle \mathbf {a} \,}$ y su módulo por ${\displaystyle a\,}$. Sus dimensiones son ${\displaystyle \scriptstyle [L\cdot T^{-2}]}$. Su unidad en el Sistema Internacional es m/s.

Fuerza Centrípeda

Se llama "fuerza centrípeta" a la fuerza o a la componente de la fuerza que actúa sobre un objeto en movimiento sobre una trayectoria curvilínea y que está dirigida hacia el centro de curvatura de la trayectoria.

El término «centrípeta» proviene de las palabras latinas centrum, «centro» y petere, «dirigirse hacia», y puede ser obtenida a partir de las leyes de Newton. En el caso de un objeto que se mueve en trayectoria circular con velocidad cambiante, la fuerza neta sobre el cuerpo puede ser descompuesta en un componente perpendicular que cambia la dirección del movimiento y uno tangencial, paralelo a la velocidad, que modifica el módulo de la velocidad.

La fuerza centrípeta no debe ser confundida con la fuerza centrífuga, tal como se explica en la sección Malentendidos comunes.

La fuerza centrípeda

Movimientos de Proyectiles

El movimiento de un proyectil es un ejemplo clásico del movimiento en dos dimensiones con aceleración constante. Un proyectil es cualquier cuerpo que se lanza o proyecta por medio de alguna fuerza y continúa en movimiento por inercia propia. Un proyectil es un objeto sobre el cual la única fuerza que actúa es la aceleración de la gravedad. La gravedad actúa para influenciar el movimiento vertical del proyectil. El movimiento horizontal del proyectil es el resultado de la tendencia de cualquier objeto a permanecer en movimiento a velocidad

El término proyectil se aplica por ejemplo a una bala disparada por un arma de fuego, a un cohete después de consumir su combustible, a un objeto lanzado desde un avión o en muchas actividades deportivas (golf, tenis, fútbol, béisbol, atletismo etc.). L os fuegos artificiales y las fuentes del agua son ejemplos del movimiento de proyectiles . El camino seguido por un proyectil se denomina trayectoria . El estudio del movimiento de proyectiles es complejo debido a la influencia de la resistencia del aire, la rotación de la Tierra, variación en la aceleración de la gravedad.





Análisis del movimiento de proyectiles

Se examina sólo trayectorias suficientemente cortas para que la fuerza gravitacional se pueda considerar constante en magnitud y dirección. También hay que analizar no tener en cuenta los efectos de la resistencia del aire; Estas hipótesis simplificadas constituyen la base de un modelo del problema físico. Como, en este caso idealizado, la única fuerza que actúa sobre el proyectil es su peso considerado constante en magnitud y dirección, es mejor referir el movimiento a un sistema de ejes coordenadas rectangulares. Se toma el eje x horizontal y el eje y verticalmente hacia arriba.
La componente x de la fuerza que actúa sobre el proyectil es nula y la componente y es el peso del proyectil – mg. Esto es, la componente horizontal de la aceleración es nula, y la componente vertical hacia abajo, es igual a la de un cuerpo que cae libremente. Puesto que la aceleración nula significa velocidad constante, el movimiento puede definirse como una combinación de movimiento horizontal con velocidad constante y movimiento vertical con aceleración constante.

Problemas de Proyectiles

Ejemplo. Se dispara un proyectil de mortero con un ángulo de elevación de 30º y una velocidad inicial de 40 m/s sobre un terreno horizontal. Calcular: a) El tiempo que tarda en llegar a la tierra; b) El alcance horizontal del proyectil.

Se tiene el valor de la magnitud de la velocidad inicial y el ángulo de elevación. A partir de ello, se pueden encontrar las componentes de la velocidad inicial Vox y Voy:

Vox = Vo cos θ = (40 m/s) cos (30º) = 34.64 m/s. (Ésta es constante)

Voy = Vo Sen θ = (40 m/s) sen (30º) = 20.0 m/s.

a) Si analizamos el tiempo en el que el proyectil tarda en llegar a la altura máxima, podemos encontrar el tiempo total del movimiento, debido a que es un movimiento parabólico completo. Suponga que tº es el tiempo en llegar a la altura máxima.

En el punto de la altura máxima, Vfy = 0 m/s. El valor de la aceleración de la gravedad, para el marco de referencia en la figura, siempre es negativo (un vector dirigido siempre hacia abajo).

De la ecuación de caída libre:

Como tº = t/2, donde t es el tiempo total del movimiento:

t = 2 * (2.04 s) = 4.08 s

b) El tiempo total del movimiento es el mismo tiempo en el que se obtiene el alcance horizontal. De M.R.U.:

d = Xmax = Vx * t = (34.64 m/s) * (4.08 s) = 141.33 m

Caida Libre y Tiro Vertical

Como la caída libre es un movimiento uniformemente acelerado en el cual la aceleración es g(aceleración de la gravedad), resultan las siguientes expresiones.

TIRO VERTICAL

Es el caso de los objetos que son lanzados verticalmente hacia arriba, por ejemplo.

• Observamos el ascenso de una cañita voladora.
• Tiramos una moneda verticalmente
• Un obrero que tira ladrillos desde el suelo al andamio.

Si la trayectoria de ese cuerpo es una linea recta vertical respecto del suelo, decimos que el cuerpo ha sido lanzado verticalmente hacia arriba.

En definitiva, cuando el proyectil o el cuerpo es lanzado hacia arriba describe una trayectoria que forma con la horizontal un angulo recto, se conoce como tiro vertical.

Al lanzar un cuerpo hacia arriba, la fuerza de gravedad actual sobre el procurando su retorno a la tierra. Es decir, la fuerza gravitatoria esta actuando negativamente, tratando de impedir ese alejamiento.

En consecuencia, si la fuerza de gravedad actúa negativamente, también la aceleración de la gravedad es negativa, por lo cual decimos que.

“Todo cuerpo lanzado verticalmente hacia arriba esta dotado de movimiento uniforme retardado”

El movimiento es uniformemente retardado, resultan las siguiente dos ecuaciones.

De las formulas se pueden llegar a unas afirmaciones interesantes, en el momento en que su velocidad final sea cero, es decir que alcanzo la altura máxima, la velocidad inicial queda igualada a la gravedad por tiempo.

Problemas de Caida Libre y Tiro Vertical

EJERCICIO 1

Supongamos que se deja caer un cuerpo desde una altura desconocida, después de transcurridos unos seis segundos el objeto toca el suelo.

1. ¿Desde que altura se soltó el objeto?
2. ¿A que velocidad llego al suelo?

RESOLUCIÓN

Veamos los datos que tenemos

• V0 = 0, la velocidad inicial del cuerpo es cero, es cuando comienza la caída.
• T = 6s, tarda seis segundo en tocar el piso

Ahora apliquemos las formulas de caída libre.

Como podemos ver este ejercicio es sencillo, pero útil para ir afianzando conceptos, por ejemplo que como la aceleración es creciente se la considera con signo positivo.

EJERCICIO 2

Se deja caer una pelota desde la punta de un edificio de 40 metros de altura, supongamos que no existe la resistencia del viento.

1. ¿Cuanto tardo la pelota en llegar al piso?
2. ¿Con que velocidad llego?

RESOLUCIÓN

Veamos los datos que tenemos

• V0 = 0, la velocidad inicial del cuerpo es cero, es cuando comienza la caída.
• Y = 40 metros

MRUA, Aceleración y Des aceleración

MRUA

El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.

Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.

También puede definirse como el movimiento que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.

El movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular del movimiento uniformemente acelerado (MUA).

La aceleración

La aceleración es la consecuencia del verbo acelerar, vocablo de origen latino, proveniente de “celer” que significa ir más rápido.

En Física se conoce como aceleración el cambio que sufre la velocidad de un cuerpo en determinado tiempo. Se necesita saber su dirección, magnitud y sentido, por tratarse de una magnitud vectorial que establece una relación entre las variaciones de velocidad y el tiempo en que tardan en producirse.. En el sistema internacional la unidad es el m/s2. Se mide con un acelerómetro. Lo que indica la aceleración es cuán rápido suceden los cambios de velocidad y no la velocidad en sí misma. Un objeto puede moverse con mucha rapidez y no ser mucha su aceleración. Si la velocidad es constante, la aceleración es igual a cero, por más que se mueva rápidamente. La aceleración negativa se denomina desaceleración. Esto sucede por ejemplo cuando un vehículo frena. El movimiento es uniformemente acelerado si el aumento es proporcional al tiempo.

La Des aceleración

Es la variación negativa de la velocidad, o sea la magnitud física que expresa el paso de un cuerpo en movimiento de una velocidad a otra velocidad inferior, siguiendo siempre la misma trayectoria. Dicho término puede definirse también como aceleración negativa.

Un ejemplo típico de des aceleración es el que ofrece un vehículo en fase de frenado. Varios son los fenómenos que se verifican en el espacio de tiempo comprendido entre el inicio de la des aceleración y la parada del vehículo. Uno de los más evidentes es el de la mayor carga que actúa sobre el puente delantero y el consiguiente aligeramiento del puente trasero.

En efecto, durante el frenado además del peso interviene la fuerza de inercia que, aplicada sobre el baricentro del coche, actúa longitudinalmente en la misma dirección que el movimiento. Dicha fuerza da lugar a un momento de vuelco longitudinal que aumenta la porción de peso del vehículo sobre las ruedas delanteras y reduce la de las traseras. Se produce, pues, lo que se define como una transferencia de carga del eje trasero al delantero.

El desplazamiento de peso determina a su vez una variación de adherencia entre las ruedas delanteras (más cargadas y por tanto más adherentes) y las traseras (menos cargadas y menos adherentes). La tendencia de las ruedas a patinar se aprecia mucho más en las traseras que en las delanteras. Por esto, muchos coches disponen de un limitador de frenado, es decir, de un dispositivo que disminuye la fuerza frenante en las ruedas traseras, reduciendo con ello el peligro de bloqueo y, por consiguiente, de deslizamiento.

Problema de Movimiento Rectilíneo Uniforme Acelerado

PROBLEMA 1

pongamos que un automóvil. parte del reposo y se acelera hasta una velocidad de 10 m/s en una trayectoria rectilínea en 5 Seg, como muestra la línea recta de la figura 1. Encontremos suaceleración media.

Figura 1

Análisis gráfico

Al observar la línea diagonal de la figura 1, notamos la variación de la velocidad y del tiempo de un automóvil que experimenta unaaceleración uniforme de 2m/s cada segundo. Esto lo podemos notar en la gráfica, ya que, el tiempo (línea horizontal) y la velocidad (línea vertical) en las parejas ordenas (0 , 0); (1 , 2); (2 , 4); (3 , 6); van variando de uno en uno el tiempo y la velocidad de dos en dos.

Análisis matemático

De la grafica podemos observar que:
V_i = 0 m/s
t = 5s
V_f =10 m/s
sustituyendo en la ecuación de la aceleración media, tenemos:

 

Lo cual lo leemos: 2 metros por Segundo cada Segundo, o 2 metros por segundo por segundo.
En otras palabras, la velocidad del automóvil se incrementen 2m/s cada segundo, y esta relación de incremento de la velocidad es la cantidad a la que se llama aceleración. El resultado anterior para ase escribe con frecuencia como 2 m/s² y se lee 2 metros porsegundos al cuadrado.

En general, la unidad de a será una unidad de distancia dividida entre el producto de dos unidades de tiempo. Las unidades podrían ser; millas por segundos cuadrados, pies por segundo por hora, centímetros por segundos por minutos, millas por hora por segundo, y así sucesivamente.

MRU, Movimiento, Distancia, Desplazamiento, Trayectoria, Rapidez y Velocidad

El movimiento rectilíneo uniforme (m.r.u.), es aquel con velocidad constante y cuya trayectoria es una línea recta. Un ejemplo claro son las puertas correderas de un ascensor, generalmente se abren y cierran en línea recta y siempre a la misma velocidad.

El movimiento

En mecánica, el movimiento es un cambio de la posición de un cuerpo a lo largo del tiempo respecto de un sistema de referencia.

El estudio del movimiento se puede realizar a través de la cinemática o a través de la dinámica. En función de la elección del sistema de referencia quedarán definidas las ecuaciones del movimiento, ecuaciones que determinarán la posición, la velocidad y la aceleración del cuerpo en cada instante de tiempo.

La distancia

En matemáticas, la distancia entre dos puntos del espacio euclídeo equivale a la longitud del segmento de la recta que los une, expresado numéricamente. En espacios más complejos, como los definidos en la geometría no euclidiana, el «camino más corto» entre dos puntos es un segmento recto con curvatura llamada geodésica.

El desplazamiento

En física, el desplazamiento, es el cambio de posición de un cuerpo entre dos instantes o tiempos bien definidos.

La trayectoria

En cinemática, trayectoria es el lugar geométrico de las posiciones sucesivas por las que pasa un cuerpo en su movimiento. La trayectoria depende del sistema de referencia en el que se describa el movimiento; es decir el punto de vista del observador.

La rapidez

La celeridad o rapidez promedio es la relación entre la distancia recorrida y el tiempo empleado en completarla. Su magnitud se designa como v. La celeridad es una magnitud escalar de dimensión. La celeridad tiene la misma dimensión que la velocidad, pero no el carácter vectorial de esta. La celeridad instantánea representa justamente el módulo de la velocidad instantánea.

La velocidad

La velocidad es una magnitud física de carácter vectorial que expresa la distancia recorrida por un objeto en la unidad de tiempo. Se representa por ${\displaystyle \mathbf {v} \,}$o ${\displaystyle {\vec {v}}\,}$(en la escritura manuscrita). Su unidad en el Sistema Internacional de Unidades es el metro por segundo (símbolo, m/s).

Problema 1

¿A cuántos m/s equivale la velocidad de un avión que se desplaza a 216 km/h?

Solución

216 km/h
=	216 *	Donde 1km = 1 000 m
=	216 000 m/h	Se cancelan los km
=	216 000 *	Donde 1h = 3 600 s
=	60 m/s	Se cancelan las h y realizamos la división

La respuesta la equivalencia, nos queda que 216 km/h = 60 m/s